Simulation von Sensordaten
Ein wichtiger Teil der Softwareentwicklung ist das Testen, dass die entwickelte Software genau das tut, was sie tun soll. In der Industrie 4.0 gestaltet sich die Suche nach passenden Testdaten allerdings häufig als schwierig. Wir zeigen deshalb ein Verfahren, mit dem Sensordaten realistisch simuliert werden können.

Die Industrie 4.0 - die Digitalisierung der industriellen Produktion - gewinnt immer mehr an Bedeutung. Dabei spielt besonders der Einsatz von Software eine wesentliche Rolle, um intelligente und digital vernetzte Systeme zu erstellen. Ein wichtiger Teil der Softwareentwicklung ist dabei das Testen mithilfe von Datensätzen, um sicherzustellen, dass die entwickelte Software am Ende auch genau das tut, was sie tun soll. Allerdings haben viele Datensätze, die dabei zum Einsatz kommen, häufig Limitierungen. Datensätze aus der “echten Welt” können zu einer Überanpassungen führen, weil die Datensätze zu spezifisch sind. Auch liegen echte Datensätze häufig in beschränkter Größe vor, wodurch sie nicht für eine umfangreiche Testung der Software ausreichen. Werden dagegen nicht echte, sondern zufällig erzeugte Daten zur Testung verwendet (z.B. numpy.random.normal), führen diese ebenfalls nicht zum erwünschten Ergebnis: Diese Daten ähneln statistischem Rauschen und verhalten sich nicht wie Daten aus der echten Welt, da ihnen die Beziehung untereinander fehlt und sie damit zusammenhanglos sind.
In diesem Blog stellen wir einen einfachen Weg vor, um kontinuierliche, normalverteilte Datensätze zu erzeugen, die echte Sensordaten realitätsnah simulieren und daher zum Testen von Software im Bereich der Industrie 4.0 besser geeignet sind. Im Gegensatz zu anderen Methoden, die normalverteilte Werte erzeugen, weisen die Daten in der hier präsentierten Methode eine Beziehung untereinander auf und sind damit Sensordaten sehr ähnlich.
Für die Codebeispiele wird C# als Programmiersprache verwendet, allerdings werden keine speziellen Eigenschaften dieser Sprache eingesetzt. Die Codebeispiele können also sehr einfach in anderen Programmiersprachen nachgebaut werden.
Anforderungen #
Zuerst definieren wir, wie die Library verwendet werden kann. Dafür legen wir die Anforderungen fest:
- Für Testzwecke ist es notwendig, denselben Datensatz öfter generieren zu können.
- Ein generierter Datensatz sollte so gut wie möglich einer Normalverteilung entsprechen.
- Ein generierter Datensatz muss sinnvoll aufeinanderfolgende Werte (ähnlich Sensordaten) erzeugen.
- Ein generierter Datensatz muss die Möglichkeit bieten, Fehler im Datensatz zu simulieren.
Deterministisches Generieren von Datensätzen #
Um die erste Anforderung zu erfüllen, bietet die Library eine Möglichkeit, den “Seed” vom Zufallszahlengenerator zu bestimmen. Auf diese Weise ist es möglich, bei jedem Aufruf das gleiche “zufällige” Ergebnis zu bekommen.
Erzeugen von normalverteilten und aufeinanderfolgenden Werten #
Klasse und Konstruktor #
Um sicherzustellen, dass diese beiden Anforderungen (Normalverteilung und aufeinanderfolgende Werte) erfüllt werden, bekommt die Klasse zwei Member-Variablen: _mean und _standardDeviation. Diese zwei Werte kommen für gewöhnlich bei der Berechnung von normalverteilten Werten zum Einsatz. Da die _standardDeviation normalerweise als Quadratwurzel der Variance berechnet wird, sind sowohl negative wie auch positive Werte möglich. Damit wir uns nicht mit den negativen Werten herumschlagen müssen, berechnen wir den Absolutwert von _standardDeviation. Dadurch bekommen wir folgende Klasse mit Konstruktor:
public class Simulator
{
private readonly Random _random;
private readonly float _mean;
private readonly float _standardDeviation;
private readonly float _stepSizeFactor;
// _value is of type double to reduce necessity of casting to float
private double _value;
public Simulator(int seed, float mean, float standardDeviation)
{
_random = new Random(seed);
_mean = mean;
_standardDeviation = Math.Abs(standardDeviation);
// we define a _stepSizeFactor that is used when calculating the
// next value
_stepSizeFactor = _standardDeviation / 10;
// we set a starting _value which is not exactly _mean (it could be
// but my personal preference is to not have each data set start on
// the same value)
_value = _mean - _random.NextDouble();
}
}Berechnen von Werten #
Als nächstes definieren wir das Interface zur Verwendung der Simulator Klasse. Der wichtige Teil ist, dass jeder Wert auf dem vorangegangenen Wert beruht und nicht als isolierter Wert in einem großen Datensatz gesehen werden sollte.
Wir definieren eine öffentliche Funktion CalculateNextValue, welche den nächsten Wert für dieses spezielle Modell liefert. Wird diese Funktion in einer Schleife aufgerufen und betrachtet man alle Werte nebeneinander, erhalten wir das erwartete Ergebnis.
Um den nächsten Wert zu berechnen, müssen wir entscheiden, um wie viel der vorangegangene Wert geändert wird und in welche Richtung (addieren oder subtrahieren) diese Änderung angewandt wird. Dafür definieren wir eine neue Member-Variable Factors, welche vom Typ List<int> ist und zwei Werte, -1 und 1 enthält.
Als nächstes schreiben wir eine neue Funktion DecideFactor, welche die Wahrscheinlichkeit berechnet, ob der vorangegangene Wert erhöht oder vermindert wird. Dafür berechnen wir - unter Berücksichtigung der _standardDeviation - die Distanz vom derzeitigen Wert zur Variable _mean.
private static readonly List<int> Factors = new(){-1, 1};
public double CalculateNextValue()
{
// first calculate how much the value will be changed
double valueChange = _random.NextDouble() * _stepSizeFactor;
// second decide if the value is increased or decreased
int factor = Factors[DecideFactor()];
// apply valueChange and factor to _value and return
_value += valueChange * factor;
return _value;
}
private int DecideFactor()
{
// the distance from the _mean
double distance;
int continueDirection;
int changeDirection;
// depending on if the current value is smaller or bigger than the mean
// the direction changes are flipped: 0 means a factor of -1 is applied
// 1 means a factor of 1 is applied
if (_value > _mean)
{
distance = _value - _mean;
continueDirection = 1;
changeDirection = 0;
}
else
{
distance = _mean - _value;
continueDirection = 0;
changeDirection = 1;
}
// the chance is calculated by taking half of the _standardDeviation
// and subtracting the distance divided by 50. This is done because
// chance with a distance of zero would mean a 50/50 chance for the
// randomValue to be higher or lower.
// The division by 50 was found by empiric testing different values
double chance = (_standardDeviation / 2) - (distance / 50);
double randomValue = _random.NextDouble() * _standardDeviation;
// if the random value is smaller than the chance we continue in the
// current direction if not we change the direction.
return randomValue < chance ? continueDirection : changeDirection;
}Datensatz erstellen #
Bevor wir uns dem Erstellen von fehlerhaften Messungen (die in echten Datensätze immer zu finden sind) widmen, werfen wir einen Blick darauf, wie wir mit der bisherigen Implementierung Datensätze generieren können:
List<double> dataSet = new List<double>();
Simulator sim = new Simulator(seed: 12345, mean: 20, standardDeviation: 5);
for(int i = 0; i < 100000; i++)
{
dataSet.Add(sim.CalculateNextValue);
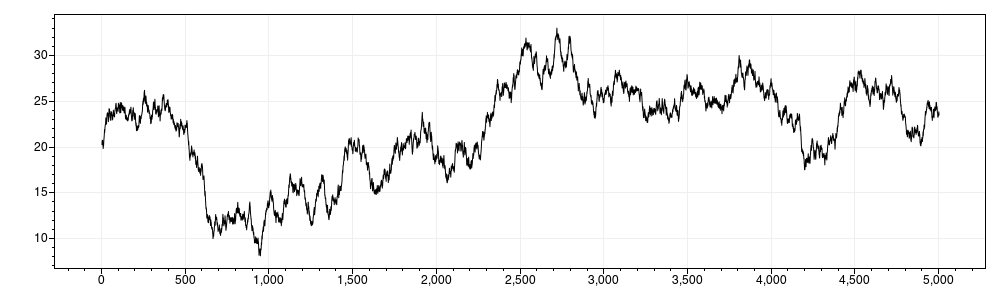
}Wenn wir diesen Beispiel-Code ausführen, bekommen wir folgendes Ergebnis: Plot der ersten 5000 Werte aus dem Ergebnisdatensatz:
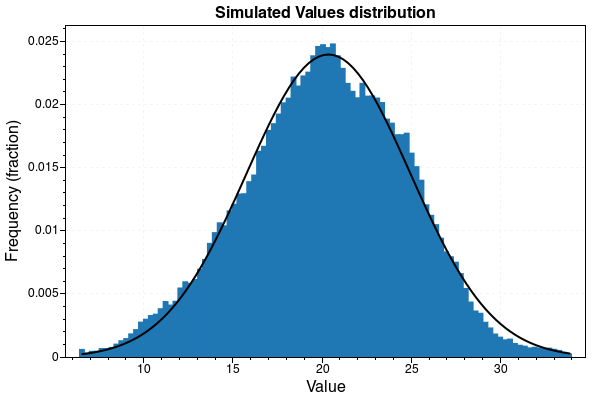
Histogramm vom gesamten Ergebnisdatensatz:
Anhand von diesem Beispiel kann man sehen, dass die individuellen Werte sich verhalten wie zum Beispiel die Werte, die ein Temperatursensor ausgibt. Wenn man dann die Verteilung aller Werte betrachtet, ergibt sich eine Normalverteilung.
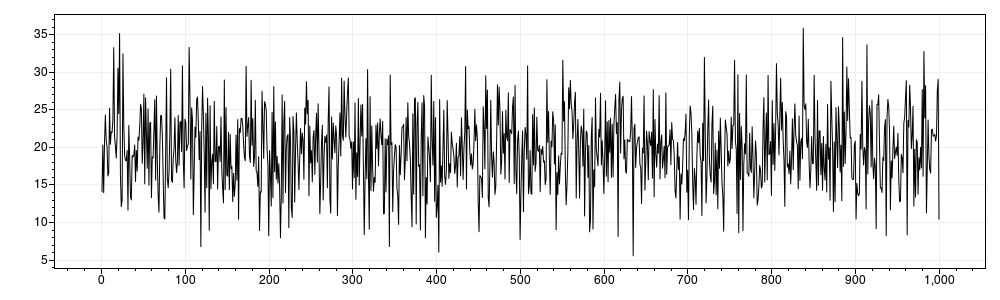
Im Vergleich dazu findet sich in folgendem Bild das Ergebnis, wenn man einen gleich großen Datensatz mit denselben Parametern mit MathNet.Numerics.Distributions.Normal generiert: Plot der ersten 5000 Werte aus dem Ergebnisdatensatz:
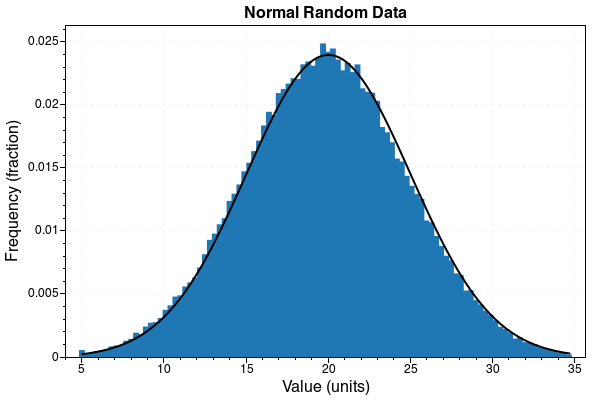
Histogramm vom gesamten Ergebnisdatensatz:
Während das Histogramm sehr ähnlich ist, haben die einzelnen Werte keinen Zusammenhang mit den benachbarten Werten und resultieren in Datenrauschen.
Hinzufügen von fehlerhaften Werten #
Eine Sache, die Daten aus der echten Welt nahezu immer enthalten, sind Fehler. Um eine Art Fehlverhalten zu simulieren, fügen wir vier optionale Parameter zum Konstruktor hinzu: errorRate, errorLength, min und max.
errorRate ist eine Dezimalzahl, welche die Wahrscheinlichkeit definiert, dass ein Fehler auftritt. Zum Beispiel ein Wert von 0.1 bedeutet, es besteht eine Wahrscheinlichkeit von 10%, dass der nächste Wert fehlerhaft ist. errorLength is eine Dezimalzahl, welche definiert, für wie lange ein aufgetretener Fehler ansteht. Zum Beispiel 4.5 bedeutet, dass wenn ein Fehler auftritt, zumindest die nächsten vier Werte ebenfalls Fehler sind und der fünfte Wert eine 50%-ige Fehlerwahrscheinlichkeit hat. Danach haben alle darauf folgenden Werte eine Fehlerwahrscheinlichkeit von einem Prozent.
min und max definieren die äußeren Grenzen für fehlerhafte Werte. Die inneren Grenzen werden durch den dreifachen Abstand der _standardDeviation vom _mean bestimmt. Dadurch sieht unsere Klasse nun folgendermaßen aus:
public class Simulator
{
private readonly float _mean;
private readonly float _standardDeviation;
private readonly float _stepSizeFactor
private double _value;
private readonly float _defaultErrorRate;
private readonly float _defaultErrorLength;
private float _currentErrorRate;
private float _currentErrorLength;
private readonly float _minimum;
private readonly float _maximum;
private bool _isCurrentError;
// we use the _lastNoneErrorValue variable to reset to this value
// after the error state ends
private double _lastNoneErrorValue;
private static readonly List<int> Factors = new(){-1, 1};
private readonly Random _random;
// we use the following variables to keep track how many errors we
// encountered
public int ValueCount { get; private set; }
public int ErrorCount { get; private set; }
public Simulator(int seed,
float mean,
float standardDeviation,
float errorRate = 0f,
float errorLength = 0f,
float minimum = float.MinValue,
float maximum = float.MaxValue)
{
_random = new Random(seed);
_mean = mean;
_standardDeviation = Math.Abs(standardDeviation);
_stepSizeFactor = _standardDeviation / 10;
// we use default and current error variables to reset the values
// after the error state ends
_defaultErrorRate = errorRate;
_defaultErrorLength = errorLength;
_currentErrorRate = errorRate;
_currentErrorLength = errorLength;
_minimum = minimum;
_maximum = maximum;
// initially we mark our state as no current error
_isCurrentError = false;
_value = _mean - _random.NextDouble();
}
}Durch diese Änderungen muss in der CalculateNextValue Funktion zwischen normalen und fehlerhaften Werten unterschieden werden. Aus diesem Grund wird der Code, der normale Werte berechnet, in eine private Funktion NextValue ausgelagert und zusätzlich eine neue private Funktion NextErrorValue geschrieben. Die Logik, welche der Funktionen für den nächsten Wert ausgeführt wird, wird in der CalculateNextValue Funktion implementiert.
public double CalculateNextValue()
{
// first we need to figure out if we are in a state of error and adjust the values
// accordinglyif (_isCurrentError)
{
_currentErrorLength -= 1;
_currentErrorRate = _currentErrorLength;
if (_currentErrorRate < 0.01)
{
_currentErrorRate = 0.01f;
}
}
// we calculate if the next value will be an error
bool nextIsError = _random.NextDouble() < _currentErrorRate;
// if not we calculate a new value and if the previous value has been an error
// we reset the error variables
// otherwise we save the _lastNoneErrorValue and calculate a new error value
if (!nextIsError)
{
NewValue();
if (_isCurrentError)
{
_isCurrentError = false;
_currentErrorRate = _defaultErrorRate;
_currentErrorLength = _defaultErrorLength;
}
}
else
{
if (!_isCurrentError)
{
_lastNoneErrorValue = _value;
}
NewErrorValue();
}
return _value;
}
private void NewValue()
{
// we increase the count of none error values
ValueCount += 1;
double valueChange = _random.NextDouble() * _stepSizeFactor;
int factor = Factors[DecideFactor()];
// if the previous value has been an error, we don't take the last value but
// the _lastNoneErrorValue as basis for the new value
if (_isCurrentError)
{
_value = _lastNoneErrorValue + (valueChange * factor);
}
else
{
_value += valueChange * factor;
}
}
private void NewErrorValue()
{
// we increase the count of error values
ErrorCount += 1;
// if the previous value has not been an error we calculate a new error value
// in the set boundaries otherwise we calculate a new value based on the
// previous error value.
if (!_isCurrentError)
{
if (_value < _mean)
{
_value = _random.NextDouble() * (_mean - 3 * _standardDeviation - _minimum) + _minimum;
}
else
{
_value = _random.NextDouble() * (_maximum - _mean - 3 * _standardDeviation) + _mean + _standardDeviation;
}
_isCurrentError = true;
}
else
{
double valueChange = _random.NextDouble() * _stepSizeFactor;
_value += valueChange * Factors[_random.Next(0, 1)];
}
}Damit ist unsere Klasse abgeschlossen (den Code der ganzen Klasse findest du am Ende des Blogposts) und wir können Datensätze generieren, die fehlerhafte Werte beinhalten. Wir nehmen das vorige Beispiel und ergänzen es um die neuen Variablen:
List<double> dataSet = new List<double>();
Simulator sim = new Simulator(seed: 12345, mean: 20, standardDeviation: 5, errorRate: 0.01f, errorLength: 4.21f, min: 0, max: 40);
for(int i = 0; i < 1000; i++)
{
dataSet.Add(sim.CalculateNextValue);
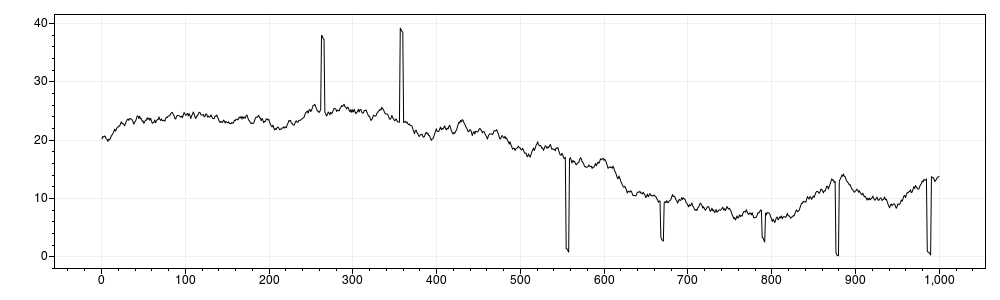
}Das Ergebnis sieht folgendermaßen aus:
Info: Das Hinzufügen von Fehlern führt dazu, dass das Histogramm keine Normalverteilung anzeigt, da die fehlerhaften Werte das Ergebnis verzerren.
Wann ist diese Methode sinnvoll #
Es macht Sinn diese Methode zur Generierung von normalverteilten Werten anzuwenden, wenn:
- Andere Libraries langsamer sind (beispielsweise benötigt MathNet doppelt so lang wie diese Methode)
- Der Datensatz soll Sensordaten simulieren und nicht nur Zufallszahlen
- Der Datensatz soll größer sein als verfügbare Datensätze
- Der Datensatz soll fehlerhafte Werte enthalten
Es macht keinen Sinn diese Methode zu verwenden, wenn:
- Der Datensatz zu 100% normalverteilt sein sollte (die hier gezeigte Methode ist nur ungefähr normalverteilt)
- Der Datensatz sich nicht wie Daten in der echten Welt verhalten soll und andere Methoden zur Datenerzeugung schneller sind
- Nur ein kleiner Datensatz benötigt wird (Normalverteilung tritt erst bei Datensätzen mit mehr als 10000 Werten auf)
Code #
namespace FloatSimulator
{
public class Simulator
{
private readonly float _mean;
private readonly float _standardDeviation;
private readonly float _stepSizeFactor;
private double _value;
private readonly float _defaultErrorRate;
private readonly float _defaultErrorLength;
private float _currentErrorRate;
private float _currentErrorLength;
private readonly float _minimum;
private readonly float _maximum;
private bool _isCurrentError;
private double _lastNoneErrorValue;
private static readonly List<int> Factors = new(){-1, 1};
private readonly Random _random;
public int ValueCount { get; private set; }
public int ErrorCount { get; private set; }
public Simulator(int seed, float mean, float standardDeviation, float errorRate = 0f, float errorLength = 0f, float minimum = float.MinValue, float maximum = float.MaxValue)
{
_random = new Random(seed);
_mean = mean;
_standardDeviation = Math.Abs(standardDeviation);
_stepSizeFactor = _standardDeviation / 10;
_defaultErrorRate = errorRate;
_defaultErrorLength = errorLength;
_currentErrorRate = errorRate;
_currentErrorLength = errorLength;
_minimum = minimum;
_maximum = maximum;
_isCurrentError = false;
_value = _mean - _random.NextDouble();
}
public double CalculateNextValue()
{
if (_isCurrentError)
{
_currentErrorLength -= 1;
_currentErrorRate = _currentErrorLength;
if (_currentErrorRate < 0.01)
{
_currentErrorRate = 0.01f;
}
}
bool nextIsError = _random.NextDouble() < _currentErrorRate;
if (!nextIsError)
{
NewValue();
if (_isCurrentError)
{
_isCurrentError = false;
_currentErrorRate = _defaultErrorRate;
_currentErrorLength = _defaultErrorLength;
}
}
else
{
if (!_isCurrentError)
{
_lastNoneErrorValue = Value;
}
NewErrorValue();
}
return _value;
}
private void NewValue()
{
ValueCount += 1;
double valueChange = _random.NextDouble() * _stepSizeFactor;
int factor = Factors[DecideFactor()];
if (_isCurrentError)
{
_value = _lastNoneErrorValue + (valueChange * factor);
}
else
{
_value += valueChange * factor;
}
}
private int DecideFactor()
{
double distance;
int continueDirection;
int changeDirection;
if (_value > _mean)
{
distance = _value - _mean;
continueDirection = 1;
changeDirection = 0;
}
else
{
distance = _mean - _value;
continueDirection = 0;
changeDirection = 1;
}
double chance = (_standardDeviation / 2) - (distance / 50);
double randomValue = _random.NextDouble() * _standardDeviation;
return randomValue < chance ? continueDirection : changeDirection;
}
private void NewErrorValue()
{
ErrorCount += 1;
if (!_isCurrentError)
{
if (_value < _mean)
{
_value = _random.NextDouble() * (_mean - 3 * _standardDeviation - _minimum) + _minimum;
}
else
{
_value = _random.NextDouble() * (_maximum - _mean - 3 * _standardDeviation) + _mean + 3 * _standardDeviation;
}
_isCurrentError = true;
}
else
{
double valueChange = _random.NextDouble() * _stepSizeFactor;
_value += valueChange * Factors[_random.Next(0, 1)];
}
}
}
}Ähnliche Blogartikel
-
 Michaela Mathis
Michaela Mathis
 Individualsoftware oder Standardsoftware: Die Entscheidung, die über Effizienz und Wettbewerbsfähigkeit entscheiden kann
Individualsoftware oder Standardsoftware: Die Entscheidung, die über Effizienz und Wettbewerbsfähigkeit entscheiden kann -
 Jürgen Fitzinger
Jürgen Fitzinger
 Unsere Erfahrungen mit Laravel - Teil 1: Setup
Unsere Erfahrungen mit Laravel - Teil 1: Setup -
 Joshua Hercher
Joshua Hercher
 Wie wir die GraphQL-Schnittstelle von Craft CMS erweitern
Wie wir die GraphQL-Schnittstelle von Craft CMS erweitern -
 Jürgen Fitzinger
Jürgen Fitzinger
 Laravel: Was es ist und wofür es verwendet wird
Laravel: Was es ist und wofür es verwendet wird