Simulation of Realistic Sensor Data
An important part of software development is testing that the developed software does exactly what it is supposed to do. In Industry 4.0, however, finding suitable test data is often difficult. We therefore demonstrate a method that can be used to realistically simulate sensor data.

An important part of the software development lifecycle is testing and making sure it behaves in an expected way. This holds true for software that is used in the Industry 4.0 but datasets for testing have problems. Real datasets are either limited in size or lead to overfitting the application to this specific dataset and randomly generated data can hide unwanted behavior by being too noisy and does not behave like real world data would.
In this blog post we discuss a simple way to generate datasets of consecutive datapoints simulating a normal distribution. Unlike other methods of generating normal distributed values (like numpy.random.normal) where the datapoints are unrelated to each other, the method used will generate values that are very similar to sensor data.
The code will be written in C# but no language specific features are used and can easily be transferred to other programming languages.
Requirements #
At first we want to define how the the library can be used. Therefore we want to define the requirements:
- For testing purposes it must be possible to generate the same result set multiple times.
- The generated dataset should be as close to normal distribution as possible
- The generated dataset must have a consecutive value flow to simulate sensor data
- The generated dataset must be able to simulate errors
Make Result Set Deterministic #
To ensure that the first requirement is fulfilled we provide a way to seed the random number generator and therefore always get the same "random" outcomes.
Generate Normal Distributed Consecutive Values #
Setting up Class and Constructor #
To ensure that these two requirements are fulfilled we set up our class to take two arguments, mean and standardDeviation. These two arguments are usually used to calculate normal distributed values. As standardDeviation is usually calculated as square root of the Variance it can be either a negative or positive value. For the sake of not having to deal with negative values we calculate the absolute value for standardDeviation.
This leaves us with the following class and constructor:
public class Simulator
{
private readonly Random _random;
private readonly float _mean;
private readonly float _standardDeviation;
private readonly float _stepSizeFactor;
// _value is of type double to reduce necessity of casting to float
private double _value;
public Simulator(int seed, float mean, float standardDeviation)
{
_random = new Random(seed);
_mean = mean;
_standardDeviation = Math.Abs(standardDeviation);
// we define a _stepSizeFactor that is used when calculating the
// next value
_stepSizeFactor = _standardDeviation / 10;
// we set a starting _value which is not exactly _mean (it could be
// but my personal preference is to not have each data set start on
// the same value)
_value = _mean - _random.NextDouble();
}
}Calculating Values #
Next we define an interface on how this Simulator class should be used. The important part is, that each value is depending on the previous value and cannot be seen as isolated value in a big set of data.
We define a public function CalculateNextValue which returns the next value for this specific model, when called in a loop and seen next to another this results in our desired dataset.
To calculate the next value we have to decide the value by which the previous value is changed and in which direction (increase or decrease) the change is done. For this we introduce a member variable called Factors which is of type List<int> and holds two values: -1 and 1.
We then create another function called DecideFactor which calculates the probability of increasing or decreasing the value by measuring the distance of the current value to the _mean and taking the _standardDeviation into account.
private static readonly List<int> Factors = new(){-1, 1};
public double CalculateNextValue()
{
// first calculate how much the value will be changed
double valueChange = _random.NextDouble() * _stepSizeFactor;
// second decide if the value is increased or decreased
int factor = Factors[DecideFactor()];
// apply valueChange and factor to _value and return
_value += valueChange * factor;
return _value;
}
private int DecideFactor()
{
// the distance from the _mean
double distance;
int continueDirection;
int changeDirection;
// depending on if the current value is smaller or bigger than the mean
// the direction changes are flipped: 0 means a factor of -1 is applied
// 1 means a factor of 1 is applied
if (_value > _mean)
{
distance = _value - _mean;
continueDirection = 1;
changeDirection = 0;
}
else
{
distance = _mean - _value;
continueDirection = 0;
changeDirection = 1;
}
// the chance is calculated by taking half of the _standardDeviation
// and subtracting the distance divided by 50. This is done because
// chance with a distance of zero would mean a 50/50 chance for the
// randomValue to be higher or lower.
// The division by 50 was found by empiric testing different values
double chance = (_standardDeviation / 2) - (distance / 50);
double randomValue = _random.NextDouble() * _standardDeviation;
// if the random value is smaller than the chance we continue in the
// current direction if not we change the direction.
return randomValue < chance ? continueDirection : changeDirection;
}Generating a Dataset #
Before we dive into generating error values a quick example is shown how to generate a data set using this method:
List<double> dataSet = new List<double>();
Simulator sim = new Simulator(seed: 12345, mean: 20, standardDeviation: 5);
for(int i = 0; i < 100000; i++)
{
dataSet.Add(sim.CalculateNextValue);
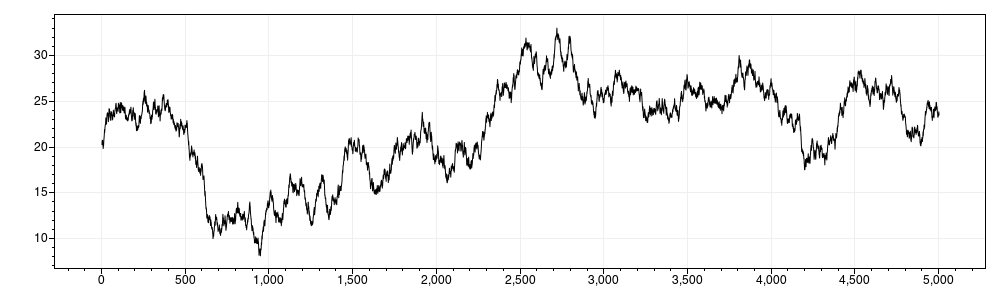
}Running this example generates the following output: Plot of the first 5000 values of the result set:
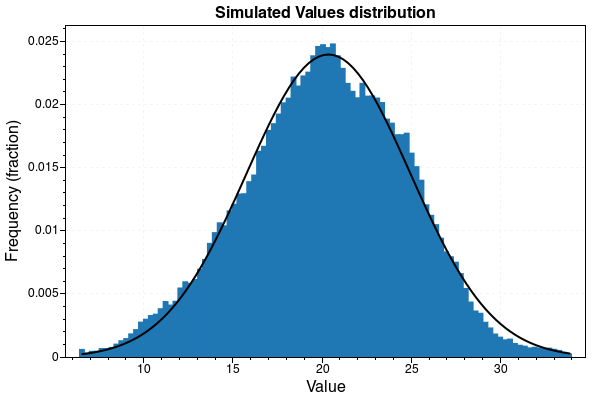
Histogram of the result set:
As you can see the individual values behave like e.g. values of a temperature sensor might behave and combining all values together results in a normal distribution.
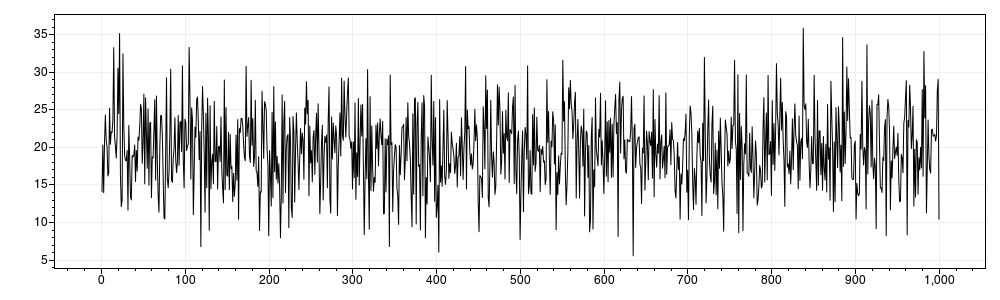
Compare this to using the same parameters and letting the values be generated by MathNet.Numerics.Distributions.Normal: plot of the first 5000 values of the result set:
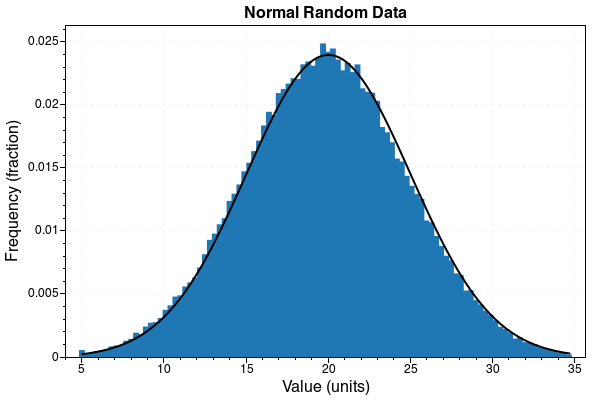
Histogram of the result set:
While the histogram looks really similar the values plotted by occurrence have no connection with the other values and result in data noise.
Introducing Value Errors #
One thing real world data almost always contains is errors. Therefore we want to be able to simulate some kind of error behavior. We introduce 4 optional parameters to the constructor, errorRate, errorLength, min and max.
errorRate is a float which defines the chance of an error happening, e.g. 0.1 means there is a 10% chance of an error happening. errorLength is a float which defines for how long an error when encountered is sustained, e.g. 4.5 means that an error is at least 4 values long and on the 5th value there is a 50% chance for another error. After that the chance for another error is always 1%.
min and max define the outer boundaries of error values. The inner boundaries are three times the standardDeviation away from the mean.
This changes our class to look like this:
public class Simulator
{
private readonly float _mean;
private readonly float _standardDeviation;
private readonly float _stepSizeFactor
private double _value;
private readonly float _defaultErrorRate;
private readonly float _defaultErrorLength;
private float _currentErrorRate;
private float _currentErrorLength;
private readonly float _minimum;
private readonly float _maximum;
private bool _isCurrentError;
// we use the _lastNoneErrorValue variable to reset to this value
// after the error state ends
private double _lastNoneErrorValue;
private static readonly List<int> Factors = new(){-1, 1};
private readonly Random _random;
// we use the following variables to keep track how many errors we
// encountered
public int ValueCount { get; private set; }
public int ErrorCount { get; private set; }
public Simulator(int seed,
float mean,
float standardDeviation,
float errorRate = 0f,
float errorLength = 0f,
float minimum = float.MinValue,
float maximum = float.MaxValue)
{
_random = new Random(seed);
_mean = mean;
_standardDeviation = Math.Abs(standardDeviation);
_stepSizeFactor = _standardDeviation / 10;
// we use default and current error variables to reset the values
// after the error state ends
_defaultErrorRate = errorRate;
_defaultErrorLength = errorLength;
_currentErrorRate = errorRate;
_currentErrorLength = errorLength;
_minimum = minimum;
_maximum = maximum;
// initially we mark our state as no current error
_isCurrentError = false;
_value = _mean - _random.NextDouble();
}
}As we now have to keep track of error values and normal values in our CalculateNextValue function we move the code to calculate normal values to a private NextValue function and create a new private function NextErrorValue to generate error values. The logic on which function to call is implemented in the CalculateNextValue function.
public double CalculateNextValue()
{
// first we need to figure out if we are in a state of error and adjust the values
// accordinglyif (_isCurrentError)
{
_currentErrorLength -= 1;
_currentErrorRate = _currentErrorLength;
if (_currentErrorRate < 0.01)
{
_currentErrorRate = 0.01f;
}
}
// we calculate if the next value will be an error
bool nextIsError = _random.NextDouble() < _currentErrorRate;
// if not we calculate a new value and if the previous value has been an error
// we reset the error variables
// otherwise we save the _lastNoneErrorValue and calculate a new error value
if (!nextIsError)
{
NewValue();
if (_isCurrentError)
{
_isCurrentError = false;
_currentErrorRate = _defaultErrorRate;
_currentErrorLength = _defaultErrorLength;
}
}
else
{
if (!_isCurrentError)
{
_lastNoneErrorValue = _value;
}
NewErrorValue();
}
return _value;
}
private void NewValue()
{
// we increase the count of none error values
ValueCount += 1;
double valueChange = _random.NextDouble() * _stepSizeFactor;
int factor = Factors[DecideFactor()];
// if the previous value has been an error, we don't take the last value but
// the _lastNoneErrorValue as basis for the new value
if (_isCurrentError)
{
_value = _lastNoneErrorValue + (valueChange * factor);
}
else
{
_value += valueChange * factor;
}
}
private void NewErrorValue()
{
// we increase the count of error values
ErrorCount += 1;
// if the previous value has not been an error we calculate a new error value
// in the set boundaries otherwise we calculate a new value based on the
// previous error value.
if (!_isCurrentError)
{
if (_value < _mean)
{
_value = _random.NextDouble() * (_mean - 3 * _standardDeviation - _minimum) + _minimum;
}
else
{
_value = _random.NextDouble() * (_maximum - _mean - 3 * _standardDeviation) + _mean + _standardDeviation;
}
_isCurrentError = true;
}
else
{
double valueChange = _random.NextDouble() * _stepSizeFactor;
_value += valueChange * Factors[_random.Next(0, 1)];
}
}With this our code is done. Now we can generate data sets containing errors. Taking the previous example we add values for the new variables and the output will look like this:
List<double> dataSet = new List<double>();
Simulator sim = new Simulator(seed: 12345, mean: 20, standardDeviation: 5, errorRate: 0.01f, errorLength: 4.21f, min: 0, max: 40);
for(int i = 0; i < 1000; i++)
{
dataSet.Add(sim.CalculateNextValue);
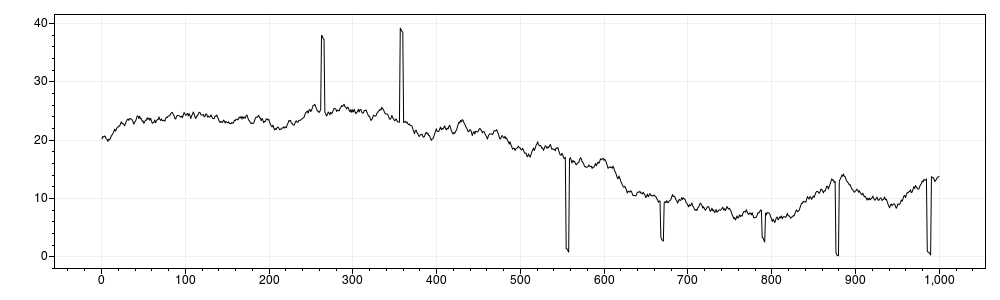
}The result will look like this:
Note: Adding errors will lead to the histogram no longer displaying a normal distribution because the error values distort the result.
When to Use This Method of Generating Normal Distributed Data #
You should use this method of generating normal distributed data when:
- other libraries are slower (e.g. MathNet takes two times longer than this method)
- you want to simulate sensor values and not just have random data
- you want to generate bigger data sets than you have available
- you want to add error elements to your data
You should not use this method when:
- you need 100% normal distributed data (this method is only approximately normal distributed)
- you don't need data that behaves like real world data and other methods are faster
- you want small data sets (normal distribution cannot be guaranteed for data sets of fewer than 10.000 values)
Code #
namespace FloatSimulator
{
public class Simulator
{
private readonly float _mean;
private readonly float _standardDeviation;
private readonly float _stepSizeFactor;
private double _value;
private readonly float _defaultErrorRate;
private readonly float _defaultErrorLength;
private float _currentErrorRate;
private float _currentErrorLength;
private readonly float _minimum;
private readonly float _maximum;
private bool _isCurrentError;
private double _lastNoneErrorValue;
private static readonly List<int> Factors = new(){-1, 1};
private readonly Random _random;
public int ValueCount { get; private set; }
public int ErrorCount { get; private set; }
public Simulator(int seed, float mean, float standardDeviation, float errorRate = 0f, float errorLength = 0f, float minimum = float.MinValue, float maximum = float.MaxValue)
{
_random = new Random(seed);
_mean = mean;
_standardDeviation = Math.Abs(standardDeviation);
_stepSizeFactor = _standardDeviation / 10;
_defaultErrorRate = errorRate;
_defaultErrorLength = errorLength;
_currentErrorRate = errorRate;
_currentErrorLength = errorLength;
_minimum = minimum;
_maximum = maximum;
_isCurrentError = false;
_value = _mean - _random.NextDouble();
}
public double CalculateNextValue()
{
if (_isCurrentError)
{
_currentErrorLength -= 1;
_currentErrorRate = _currentErrorLength;
if (_currentErrorRate < 0.01)
{
_currentErrorRate = 0.01f;
}
}
bool nextIsError = _random.NextDouble() < _currentErrorRate;
if (!nextIsError)
{
NewValue();
if (_isCurrentError)
{
_isCurrentError = false;
_currentErrorRate = _defaultErrorRate;
_currentErrorLength = _defaultErrorLength;
}
}
else
{
if (!_isCurrentError)
{
_lastNoneErrorValue = Value;
}
NewErrorValue();
}
return _value;
}
private void NewValue()
{
ValueCount += 1;
double valueChange = _random.NextDouble() * _stepSizeFactor;
int factor = Factors[DecideFactor()];
if (_isCurrentError)
{
_value = _lastNoneErrorValue + (valueChange * factor);
}
else
{
_value += valueChange * factor;
}
}
private int DecideFactor()
{
double distance;
int continueDirection;
int changeDirection;
if (_value > _mean)
{
distance = _value - _mean;
continueDirection = 1;
changeDirection = 0;
}
else
{
distance = _mean - _value;
continueDirection = 0;
changeDirection = 1;
}
double chance = (_standardDeviation / 2) - (distance / 50);
double randomValue = _random.NextDouble() * _standardDeviation;
return randomValue < chance ? continueDirection : changeDirection;
}
private void NewErrorValue()
{
ErrorCount += 1;
if (!_isCurrentError)
{
if (_value < _mean)
{
_value = _random.NextDouble() * (_mean - 3 * _standardDeviation - _minimum) + _minimum;
}
else
{
_value = _random.NextDouble() * (_maximum - _mean - 3 * _standardDeviation) + _mean + 3 * _standardDeviation;
}
_isCurrentError = true;
}
else
{
double valueChange = _random.NextDouble() * _stepSizeFactor;
_value += valueChange * Factors[_random.Next(0, 1)];
}
}
}
}

 Michaela Mathis
Michaela Mathis

 Jürgen Fitzinger
Jürgen Fitzinger


